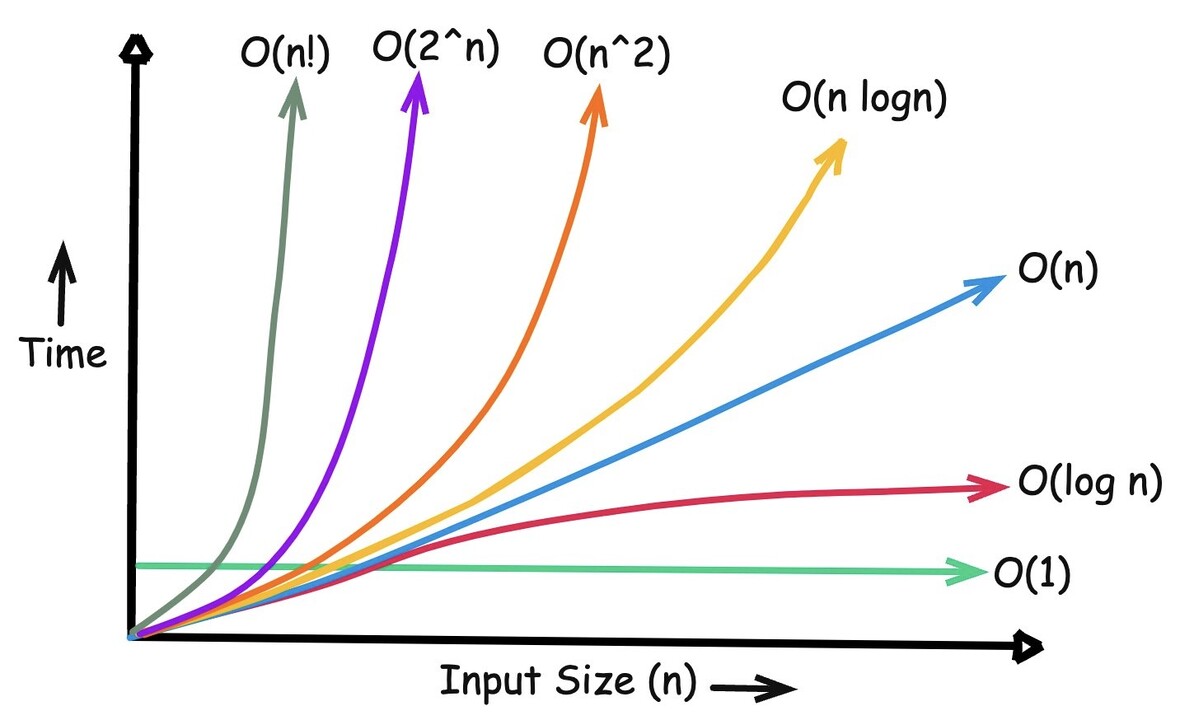
Notación Big O
Hay distintas formas de analizar que tan bueno es un algoritmo, la notación más común en los desafíos de programación es la notación Big O. La cual indica cuánto es lo máximo que puede tomar en ejecutar un algoritmo.
Utilizarla permite saber si la solución propuesta estará dentro de los límites permitidos sin necesidad de ejecutar la solución.
Las más comunes son: , , , .
Los poco comunes son: , , .
Constante
Tiempo de ejecución constante. Es lo más rápido y una solución que logre este tiempo es ideal.
Normalmente soluciones que ocupen fórmulas matemáticas pueden alcanzar este tiempo de ejecución ya que no ocupan bucles, solo operaciones artiméticas.
Como ejemplo se da el cálculo de celcius a farenheit.
#include <iostream>
using namespace std;
int main() {
long long celcius, farenheit;
cin >> celcius;
farenheit = (celcius * 1.8) + 32;
cout << farenheit << endl;
return 0;
}Algoritmos :
-
Acceder un elemento de un arreglo (
array[5]). -
Insertar un nodo en una lista enlazada (linked list)
-
Push (añadir) y Pop (sacar) en un stack (pila).
-
Insertar y remover de una Queue (cola).
-
Encontrar el padre o hijos izquierdo/derecho de un nodo dentro de un árbol almacenado en un arreglo.
-
Saltar al elemento siguiente o anterior dentro de una lista doblemente enlazada. (Doubly linked list)
Logarítmica
Tiempo de ejecución logarítmico. Es similar a con la diferencia que disminuye en el tiempo. Es decir la velocidad de ejecución disminuye en el tiempo debido a que existen menos elementos para evaluar.
Algoritmos :
-
Búsqueda binaria.
-
Encontrar el número más grande / más pequeño dentro de un árbol de búsqueda binario (binary search tree).
-
Algunos algoritmos de divide y vencerás basados en funciones lineales.
-
Cálculo de fibonacci optimizado.
Lineal
Tiempo de ejecución lineal. Es lo más común. La solución
tardará tanto como elementos se deba procesar. Normalmente
identificadas por la utilización de un bucle for o while.
#include <iostream>
using namespace std;
int main() {
long long n, i;
cin >> n;
for(i = 0; i < n; i++) {
cout << i << endl;
}
return 0;
}Algoritmos :
-
Iterar un arreglo.
-
Iterar una lista enlazada.
-
Búsqueda lineal.
-
Eliminar un elmento específico en una lista enlazada (sin ordenar).
-
Comparación de dos strings.
-
Detección de un palíndromo.
-
Conteo de elementos / Bucket sort.
Cuasilineal
Algoritmos :
-
Merge Sort.
-
Heap Sort.
-
Quick Sort.
-
Algunos algoritmos de divide y vencerás basados en tiempo cuadrático.
Cuadrática
Algoritmos :
-
Bubble Sort.
-
Insertion Sort.
-
Selection Sort.
-
Navegar un arreglo 2D (
array[x][y]) asumiendo que ambos arreglos sean de dimensión. Puede depender de cada cantidad de elementos del arreglo .
Exponencial
La complejidad exponencial aparece cuando se deben explorar todas las combinaciones (combinatoria) posibles de un conjunto de elementos. Mientras mayor sea la entrada, mayor es el tiempo de ejecución.
El ejemplo muestra un fibonacci no optimizado (ingenuo) que genera todas las posibilidades, creciendo exponencialmente. Cada vez ejecutará dos veces el mismo algoritmo, generando todos los números cada vez.
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n - 1) + fibonacci(n - 2)Algoritmos :
-
Algoritmos de fuerza bruta para problemas NP-Completos.
-
Problema de la mochila (sin memoización).
-
Generación de subconjuntos (Power Set).
-
TSP (traveling salesman) si se usa programación dinámica.
Factorial
Es el peor tiempo de ejecución. Crecen en complejidad aún más rápido que los exponenciales. Normalmente aparecen al necesitar calcular todas las permutaciones (permutación) de un conjunto de elementos.
Algoritmos :
-
Búsqueda de fuerza bruta en el problema del vendedor ambulante (traveling salesman).
-
Generación de permutaciones en un conjunto parcialmente ordenado.
-
Encontrar el determinante con la expanción de Laplace.